長方形のヨコの長さをa、タテの長さをbとすると、 √(a^2 b^2) で計算できちゃうんだよ。 つまり、 √( タテ×タテ ヨコ×ヨコ) になるわけさ。 たとえば、ヨコの長さが4cm、 タテの長さが3cmの長方形がいたとする。 対角線の長さは、 √(4^2 3^2) = √25 = 5 cm対角線=√(底辺 2 +高さ 2 ) 電卓で計算する方法 例:2×1cmの長方形の場合 2→×→=→M→ 1→×→=→M→ MR→√つまり,「対角線→四角形」の順です。 はじめは同じ長さの棒を使って四角形を作りま す。正方形・長方形・台形はできますが,平行四辺 形やひし形はできません。「ちがう長さの棒がほし い」という子どもたちの声に答えて別の棒をわたす

中3数学 相似 台形の対角線 Youtube
対角線 長さ 等しい 四角形
対角線 長さ 等しい 四角形-四角形 abcd において,対角線 bd , ac の中点をそれぞれ q , s ,辺 ad , bc の中点をそれぞれ p , r とする. ab=6 , bc=10 , cd=8, da=4 とするとき,次の辺の長さを求めなさい. _____ pq=rs= _____ qr=sp= (これらから四角形 pqrs は平行四辺形であることが言えます.)対角線の長さが4cmの正方形の辺の長さを求める 例題2 ある正方形における対角線の長さは4cmです。 四角形の対角線の性質について学びます。 2 基礎がある程度水平な状態で固まったあと、まず最初に(ご存知かも知れません が)一番大事なことは、並べていく方向に糸を張ること。 8cmに相当
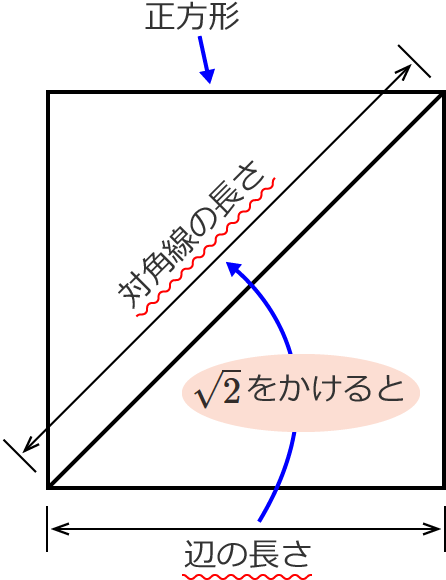



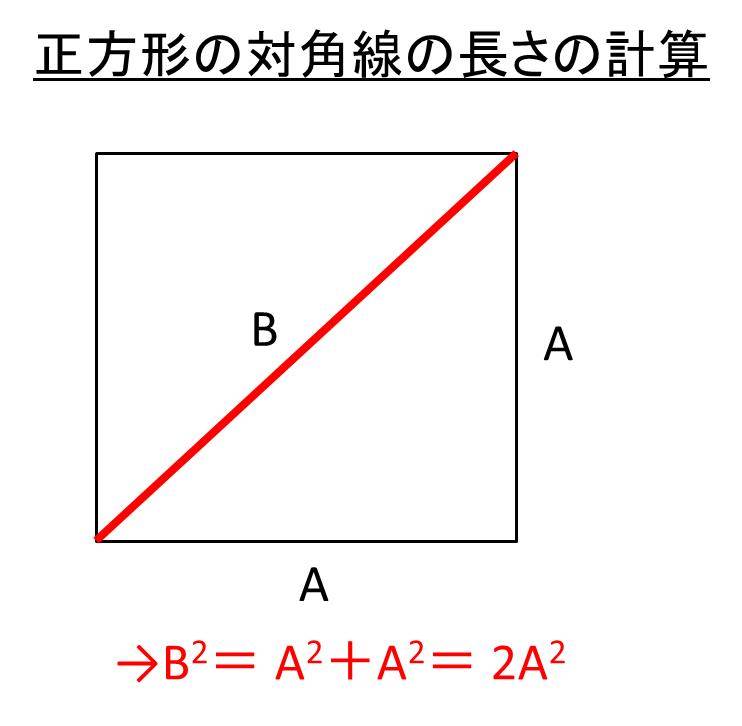
正方形の対角線の長さの求め方
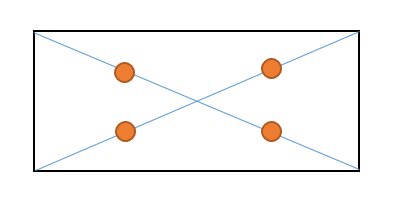
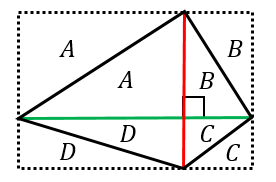
対角線 四角形の、向かい合う頂点同士をむすんだ直線のことを、対角線といいます。 ・2本の対角線が、それぞれのまん中の点で交わる四角形平行四辺形、ひし形、長方形、正方形 ・2本の対角線の長さが等しい四角形長方形、正方形対角線は(2本あるが、そのどちらも)他の対角線の中点を通る。対角線は、互いの長さを2 等分する。 凹四角形 内角の大きさが180°(π ラジアン) を超えるような頂点を持つ四角形。対角線が四角形の内部で交点を持たない、外角が定義できないなどの不都合があるため、日本の初等中等教育では「矢じり形」などと呼んで、四角形の集合には含めない。対角線の長さと交わる角度から、四角形の面積を求める問題。 一発では求められないので、図Aで色分けしたような4つの三角形に分けて考えよう。 三角形の面積の公式はいくつかあるけど、ここでは 公式
四角形の4つの辺の長さ \(a,b,c,d\) に加え、どちらか一方の対角線の長さ \(e\) が分かっている場合。 四角形を2つの三角形に分けてから各三角形の面積 \(S_1,S_2\) をヘロンの公式を使って求め、それらを合計することで四角形の面積を求めることができます。対角線の長さが等しく、それぞれの中点で交わるとき長方形になる。 証明 それぞれの中点で交わるので四角形abcdは平行四辺形になる。 abcと dcbで 平行四辺形abcdの性質より ab=dc 1 bc=cb(共通) 2 仮定(対角線の長さが等しい)より正方形 ⇒ 全ての辺の長さ・角度が等しい四角形 ひし形と対角線の関係 ひし形の対角線は直角に交わります。下図をみてください。ひし形に対角線を2本引きました。 このとき対角線は中点(真ん中の点)で交わります。よって4つの三角形の斜辺、底辺
対角線の交わり方に気をつけて四角形を作っていた。 対角線の長さや交わらせ方によって、指定された四角形ができたりできなかったりする。 対角線の交わり方が垂直かどうか、交わった点からの長さが等しいかどうかに気をつけながら、形作りをした。 形ができたところで、対角線の交わり②対角線の長さは対抗する辺の長さの合計に依存して変化可能。 ③三角形AEDの面積は辺dが一定なのでL1、L4の積に比例する。 ④三角形BECの面積も辺bが一定なのでL2,L3の積に比例する。 ⑤三角形ABE、CDEも同様にL1,L3 L2、L4の積に比例する。 結論として四角形の2つの対角線の長さの積が最四角形は,1つの対角線で2つの三角形に分けることができます。 平行四辺形,ひし形,長方形,正方形は,1つの対角線で,形も 大きさも同じ2つの三角形に分けることができます。 trsA6F3tmpjtd 岩倉市日本語・ポルトガル語適応指導教室




勉強しよう数学 円に内接する四角形の対角線の交差点までの長さ
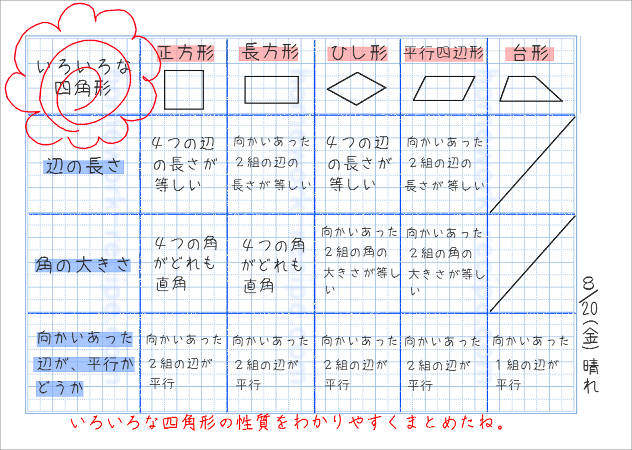



いろいろな四角形の性質をノートにまとめよう 家庭学習レシピ
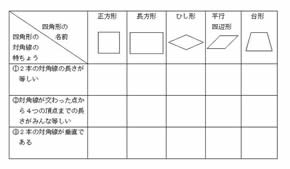
四角形の対角線の交点を \(p\)、\(ad,bc\) の延長上の交点を \(x\) とおいたとき \(pa×pc=pb×pd\) \(xa×xd=xb×xc\) 方べきの定理については、以下のページで詳しく解説しています。 方べきの定理とは?3つのパターンの図解とその証明方法 1つの円に2本の直線を引いたときに作らオンラインの長方形の計算機を使用して、長方形の面積、周囲、および対角線を計算します。 矩形 ジオメトリでは、長方形は4つの内角すべてが90°(直角)の四角形です。 フォーミュラ 以下は、辺の幅がa、長さがbの長方形の面積、周囲、対角線の計算式2本の対角線が交わった点から4つの頂 点までの長さが等しい。 2本の対角線が垂直に交わっている。 2) 教科書128ページの四角形に対角線をかいてとくちょうを調べ、 まとめます 。あてはまるところに をかこう 台形 平行 ひし形 長方形 正方形 2本の対角線の
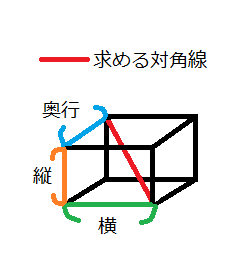



直方体の対角線の長さ 高精度計算サイト




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ
要約欄への記入を参照ください。翻訳後、 翻訳告知 Orthodiagonal quadrilateral をノートに追加することもできます。Wikipedia 翻訳のガイドラインに、より詳細な翻訳の手順・指針についての説明があります。 直交対角線四角形 正方形に内接する直交対角線四角形。 対角線bdをひくところから証明していきましょう。 個別指導塾の基本問題に挑戦! 問題 下の図のような四角形abcdがあり、点e、f、g、hはそれぞれ各辺の中点であるとする。このとき、四角形efghが平行四辺形であることを、以下のように証明した。( )内に1 円に内接する四角形の対角線について 1 円に内接する四角形の対角線について 円に内接する四角形abcdの対角線の交点をe




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ
平行四辺形の対角線の条件に、「 2本の対角線の長さが等しい 」 と言う条件が加われば、長方形になります。 平行四辺形の対角線の条件に、「 2本の対角線の長さが等しい 」 「 2本の対角線が垂直 ( 90° ) に交わる 」 と言う2つの条件が加われば、正方形になります。 正方形、長方形、ひし形はいずれも平行四辺形であり、平行四辺形の中でも、一定の条件対角線は(2本あるが、そのどちらも)他の対角線の中点を通る。対角線は、互いの長さを2 等分する。 凹四角形 内角の大きさが180°(π ラジアン) を超えるような頂点を持つ四角形。対角線が四角形の内部で交点を持たない、外角が定義できないなどの不都合があるため、日本の初等中等教育では「矢じり形」などと呼んで、四角形の集合には含めない。その通りですが、「たこ型」はどちらかと言うと 『対角線が垂直に交わる四角形はひし形』 の反例としてよく使われますよね。 等脚台形も対角線の長さは等しいわけですし。 対角線が「等しい」「垂直に交わる」が、それぞれ「長方形」「ひし形」になるためには、その四角形が 「平行四辺形である」 (対角線がそれぞれの中点で交わる) という条件が必要です



変形の四角形の対角線の求め方を教えてください 添付画像のような図形 Yahoo 知恵袋
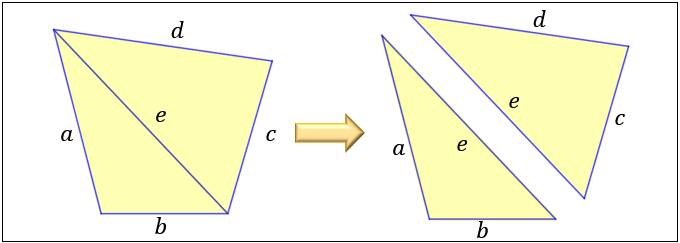



四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
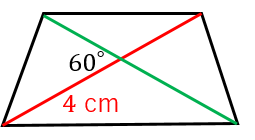
直交対角線四角形の面積Kは、対角線pとqの長さの積の半分で求められる 。 K = p × q 2 {\displaystyle K={\frac {p\times q}{2}}} 逆に、この式で面積を計算できる凸四角形は、対角線が直交している必要が 対角線が直交しない場合はどうすればよいでしょうか 実は対角線が直角に交わらない場合でも対角線の長さと面積の間には関係がありますただし高校数学で習う三角比の考え方が必要です どんな四角形でも対角線のなす角を theta とおくと 長方形の対角線の長さを求めるためには三平方の 対角線は(2本あるが、そのどちらも)他の対角線の中点を通る。対角線は、互いの長さを2 等分する。 凹四角形 内角の大きさが180°(π ラジアン) を超えるような頂点を持つ四角形。対角線が四角形の内部で交点を持たない、外角が定義できないなどの不都合があるため、日本の初等中等教育では「矢じり形」などと呼んで、四角形の集合には含めない。
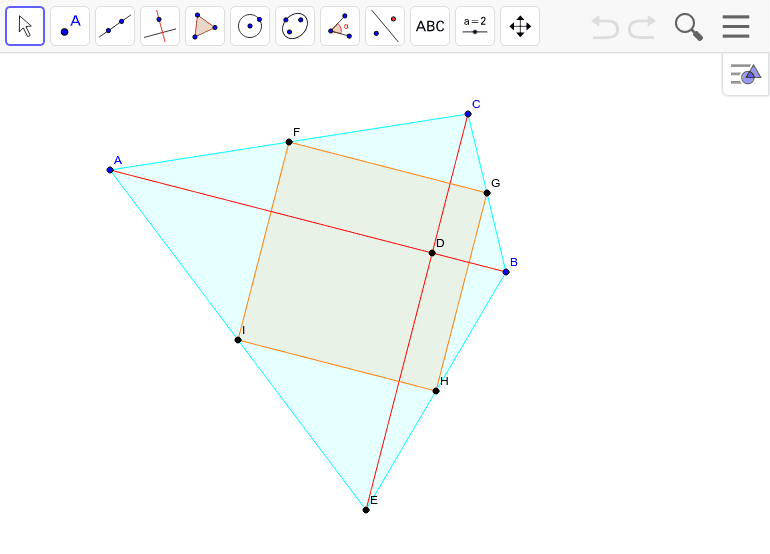



直交四角形 Geogebra




正方形の対角線で面積を求めることができる 知らない人も多いぞ 中学や高校の数学の計算問題
長方形,正方形,台形,平行四辺形,ひし形の対角線の長さや交わり方について,次のア, イ,ウにあてはまるものを選び, を書きましょう。 長方形 正方形 台形 平行四辺形 ひし形 ア 2本の対角線の長ささらに、『すべての角が直角』の長方形と『すべての辺の長さが等しい』ひし形ですが、これらの定義とは対象的に対角線については長方形が 『対角線の長さが等しい』 、ひし形が 『対角線が直交する』 という性質があります。四角形の面積(4辺と対角の和から) たまたま訪れました。 この公式は,S=absin (θ1)÷2cdsin (θ2)÷2 と比較して,誤差が小さくなるのだろうか。 対角の距離を測定する手間が省けて非常に助かります。 助かりました! アンケートにご協力頂き有り難う




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ




高校数学 対角線の長さとなす角で表された四角形の面積公式 S 1 2pqsin8 裏技 の証明 対角線の長さの和が一定である四角形の面積の最大 受験の月
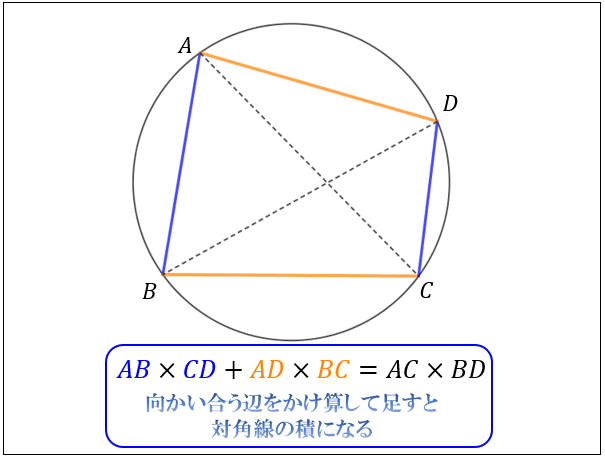
対角線の長さの積をとると、対辺の積の和になります。 これに対するわかりやすい説明はあるのでしょうか? よって、円に内接する四角形の対辺同士の積の和は、対角線の積に等しくなる。 『円に内接する四角形』へ 数学の部屋へもどる四角形で対角線の長さが等しければ 長方形である × 長方形の定理の逆 ~平行四辺形で対角線の長さが等しければ 長方形である ひし形の定理の逆 四角形で対角線が垂直に交われば ひし形である × ひし形の定理の逆 ~平行四辺形で対角線が垂直に交われば 2辺の値から四角形の対角線長を求めるiPhone向けウェブアプリ SNAPMANNE マークアップの基礎の対角線の計算 ミリの必要な寸法を選択します。 X 底辺の長さ Y 基礎の幅 特長。 財団や斜めの壁をマーキングの計算。 90 度の正確な角度を確立するために使用。 建築材料の無料サービスの計算 電卓
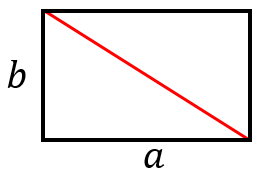



長方形の対角線の長さの求め方 具体例で学ぶ数学
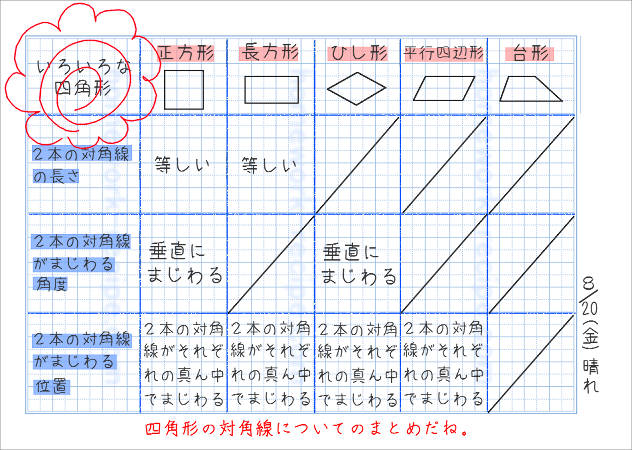



いろいろな四角形の性質をノートにまとめよう 家庭学習レシピ
平行四辺形の続き 次に,長方形,ひし形,正方形の性質を扱いましょう. 定義 1.4つの角が等しい四角形を長方形という. 2.4辺の長さが等しい四角形をひし形という. 3.4つの角が等しくかつ4辺の長さの等しい四角形を正方形という. まず,長方形(2組の対角の大きさがそれぞれ等しい長方形は円に内接する四角形なので,トレミーの定理が使えます。 長方形の辺の長さを a, b a,b a, b ,対角線の長さを c c c とおきます。トレミーの定理より「 上×下 + 左×右 =対角線のかけ算」なので a 2 b 2 = c 2 a^2b^2=c^2 a 2 b 2 = c 2 となります。これは



対角線の長さ 本数の求め方とは 公式を使って一瞬で計算しよう Studyplus スタディプラス



2本の対角線の長さが等しい四角形は長方形ですか 長方形とは限りません 例 Yahoo 知恵袋




高校数学 円に内接する四角形の対角線の長さと面積 受験の月




中学受験 算数 正方形の対角線の長さ 中高一貫 適性検査解説 Note




簡単公式 正方形の対角線の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
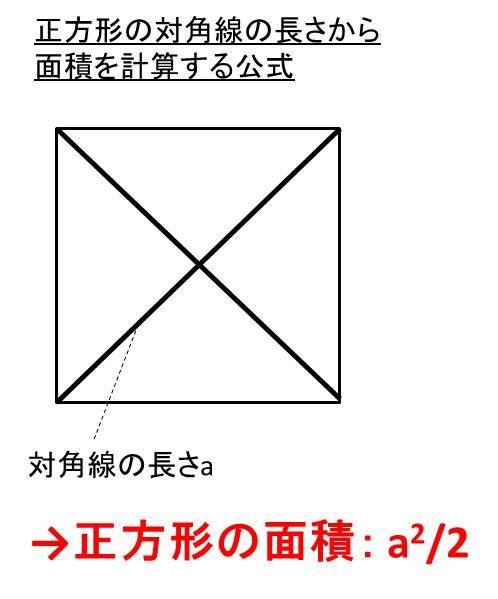



正方形で対角線の長さから面積を計算する方法 面積から対角線を求める公式 平方根 ウルトラフリーダム




小4 B 四角形 対角線 2つの対角線が真ん中で交わる 互いに垂直 同じ長さ Youtube
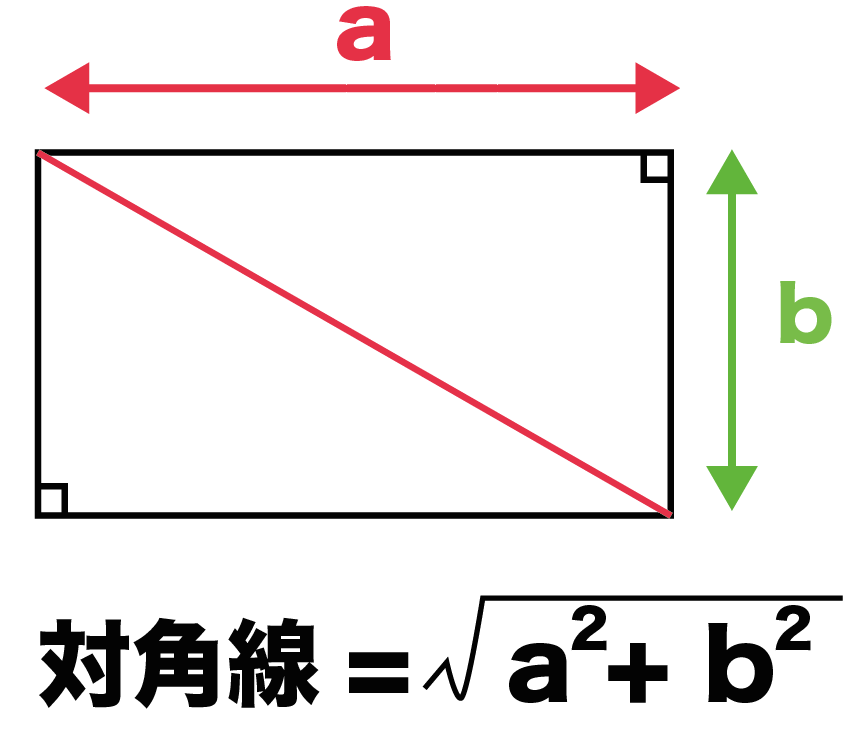



3秒で計算 長方形の対角線の求め方がわかる公式 Qikeru 学びを楽しくわかりやすく
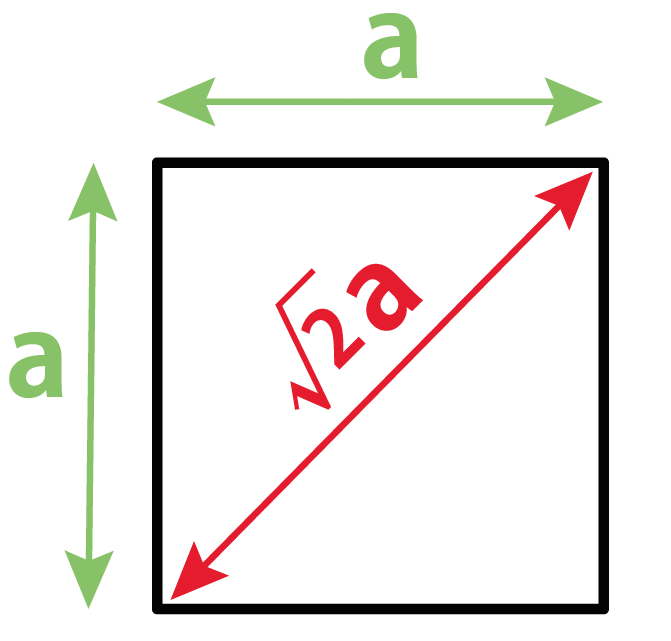



簡単公式 正方形の対角線の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



面積最大の四角形
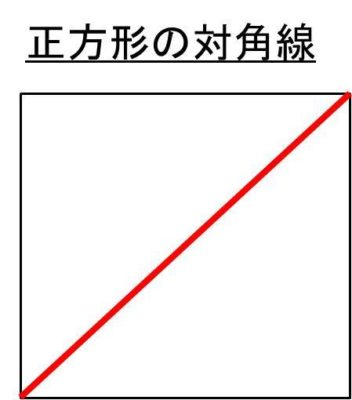



正方形の対角線の求め方と対角線から辺の長さを計算する方法 白丸くん
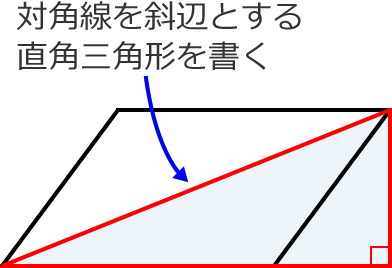



平行四辺形の対角線の長さの求め方




高校数学 数 円に内接する四角形abcdの対角線の長さと面積 Youtube



四角形 12時目



円に内接する四角形abcdにおいて 2つの対角線ac の交点を Yahoo 知恵袋



対角線の長さ 本数の求め方とは 公式を使って一瞬で計算しよう Studyplus スタディプラス



小学算数 平行四辺形 ひし形 長方形 正方形の対角線は真ん中で交わる 偏差値40プログラマー



対角線で参観 教育考現学




対角線と四角形 Youtube




3秒で計算 長方形の対角線の求め方がわかる公式 Qikeru 学びを楽しくわかりやすく



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典




四角形 Wikipedia




四角形の4辺の長さと対角線のなす角がわかっている時 対角線の長さを 数学 教えて Goo



四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




算数 小4 19 四角形の特ちょう Youtube



四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学




中3数学 相似 台形の対角線 Youtube



対角線の長さ 本数の求め方とは 公式を使って一瞬で計算しよう Studyplus スタディプラス
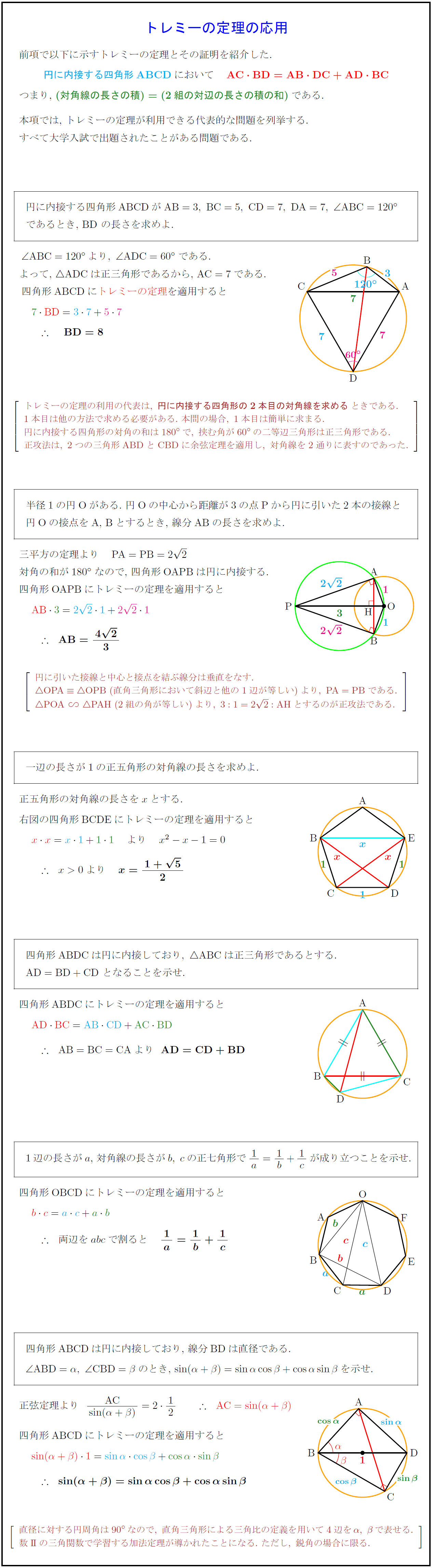



高校数学 トレミーの定理 裏技 の応用6種 円に内接する四角形の対角線の長さなど 受験の月




長方形の性質 対角線の長さはなぜ等しいのか Qikeru 学びを楽しくわかりやすく




正方形 長方形 ひし形 平行四辺形 台形と いろいろな四角形について 辺の長さ 角の大きさ そして対角線などその性質をまとめて表にかき表してみましょう 1つ1つ習って覚えてきたこと Artofit



対角線の長さ 本数の求め方とは 公式を使って一瞬で計算しよう Studyplus スタディプラス



円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ




四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
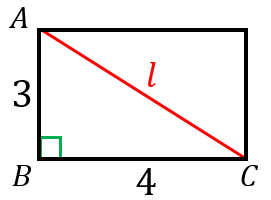



長方形の対角線の長さの求め方 具体例で学ぶ数学




3 Abcd Ab Da Descubre Como Resolverlo En Qanda




正方形の対角線の長さの求め方
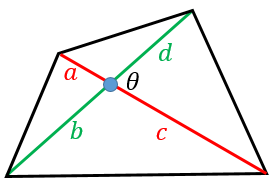



四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学



正方形の対角線の求め方と対角線から辺の長さを計算する方法 白丸くん
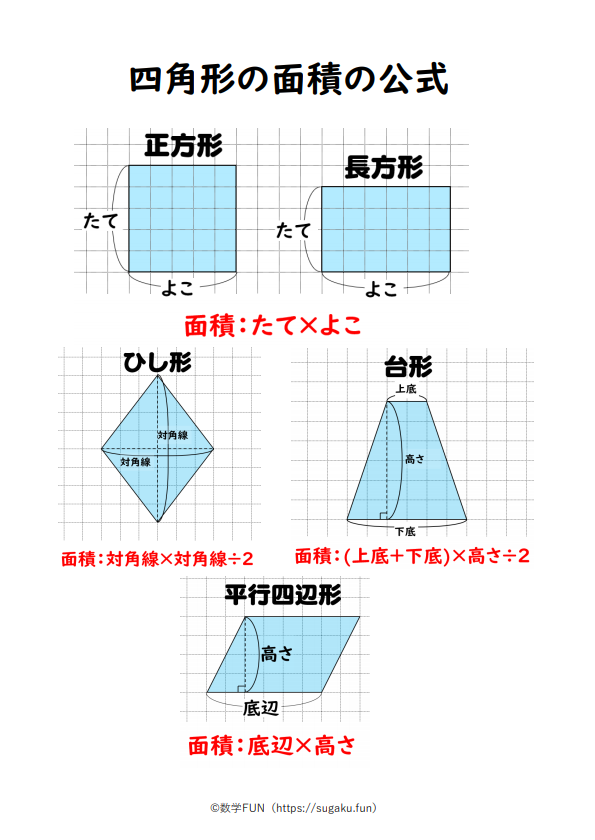



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



Q Tbn And9gcsk3iooe0glw6r2emrvfhyuy5donjyjtkxf7fg Abxgmzsqhp Usqp Cau
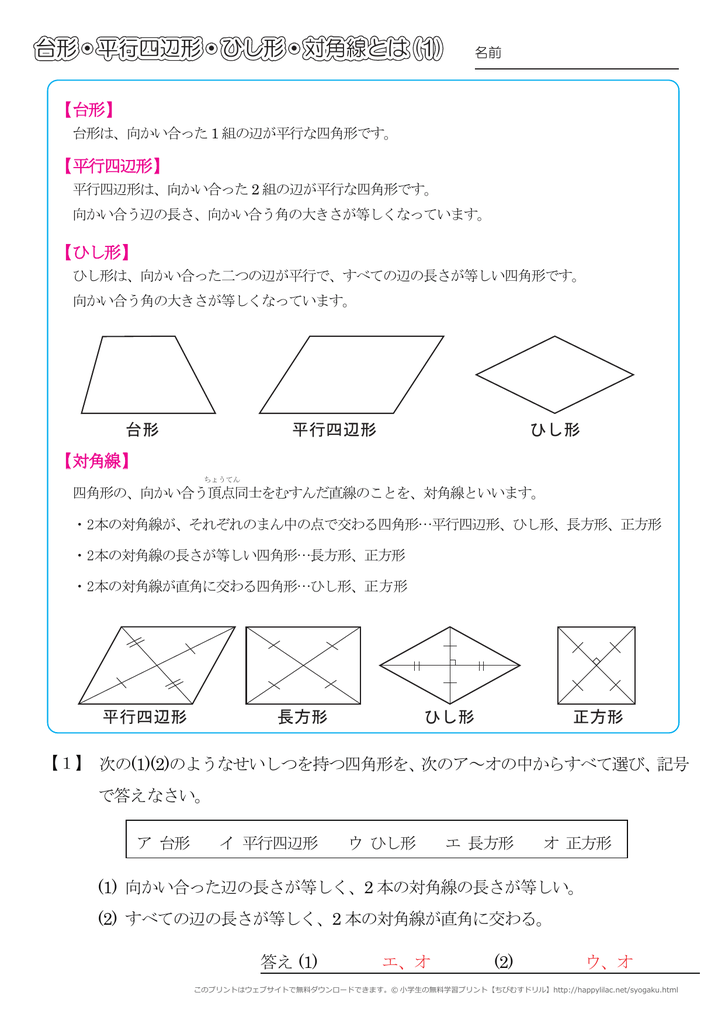



台形 平行四辺形 ひし形 対角線とは 1



数学教育 幾何 図形 的見方 四角形 分類




平行四辺形の対角線の長さの求め方



対角線の長さ 本数の求め方とは 公式を使って一瞬で計算しよう Studyplus スタディプラス



1
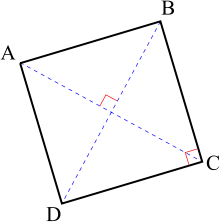



四角形 Wikipedia



1



対角線の長さ 本数の求め方とは 公式を使って一瞬で計算しよう Studyplus スタディプラス




高校数学 円に内接する四角形の計量 基本と裏技のまとめ トレミーの定理 ブラーマグプタの公式他 受験の月



平面図形の基礎



いろいろな四角形 四角形の対角線 シリウス 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材




四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
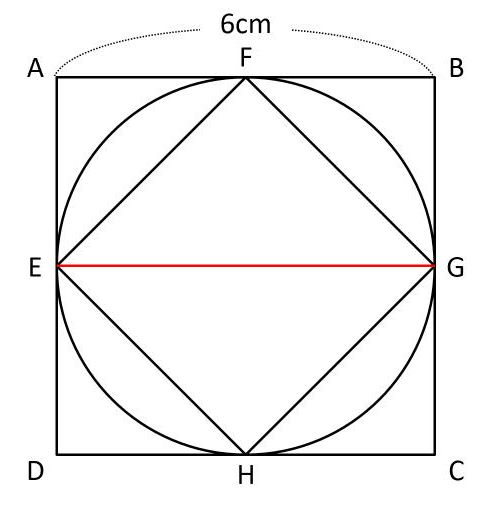



正方形の対角線の長さを求めたい 小学生が算数の知識を使ってどこまでできる 中学受験ナビ



対角線の長さ 本数の求め方とは 公式を使って一瞬で計算しよう Studyplus スタディプラス
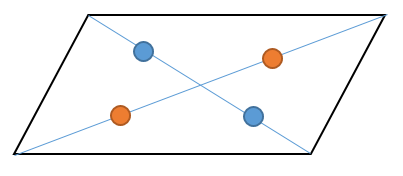



小学算数 平行四辺形 ひし形 長方形 正方形の対角線は真ん中で交わる 偏差値40プログラマー
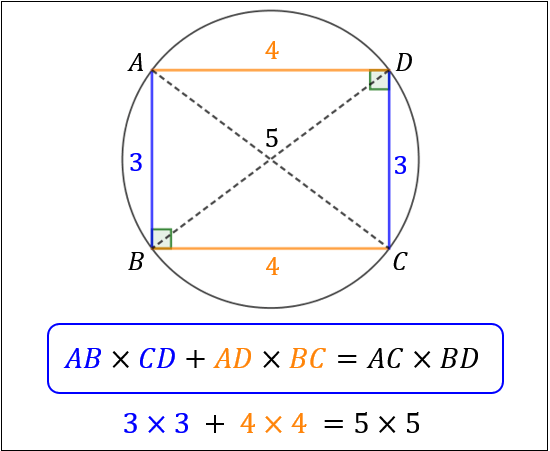



円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ
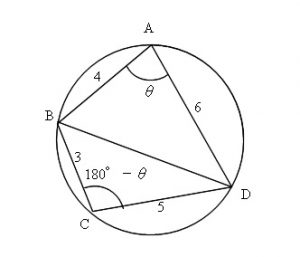



円に内接する四角形の面積の求め方と定理の使い方
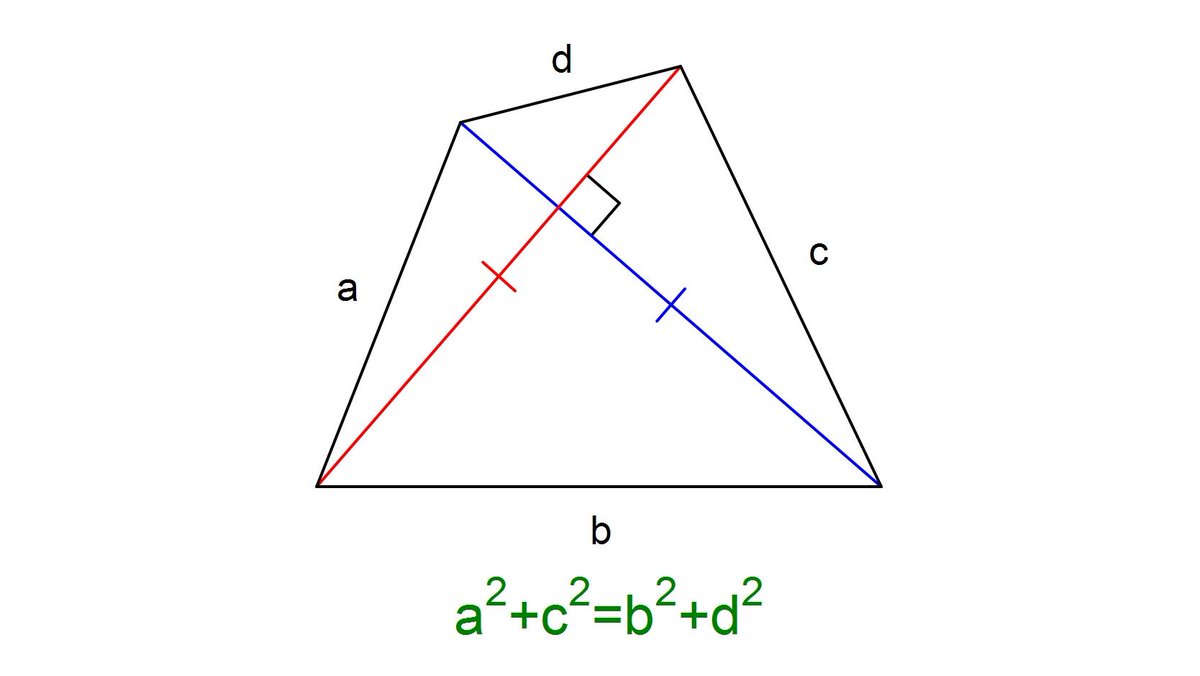



ポテト一郎 Sur Twitter 対角線の長さが等しく垂直に交わる四角形 辺の長さに次の関係があります



数学の質問です 対角線の長さが等しい四角形は 長方形である Yahoo 知恵袋




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun
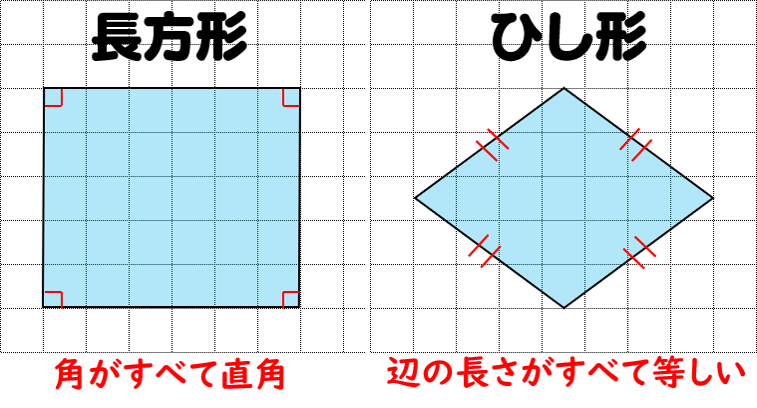



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



1




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
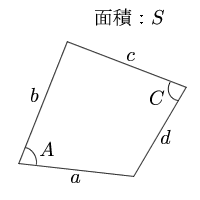



四角形 4辺と対角の和 面積の計算 計算サイト




平行四辺形の対角線の長さの求め方
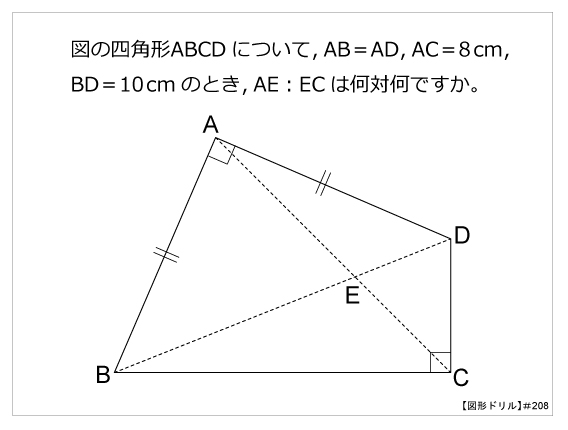



図形ドリル 第8問 四角形の対角線 算数星人のweb問題集 中学受験算数の問題に挑戦




Abcd 6 Absqrt3 Cm Da Descubre Como Resolverlo En Qanda
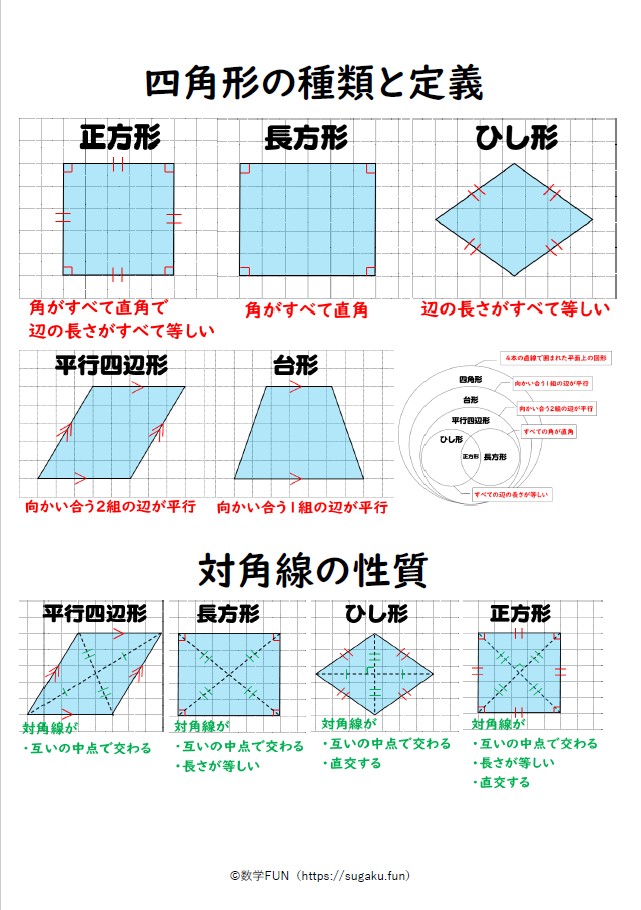



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




簡単公式 正方形の対角線の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
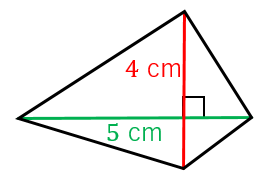



四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学
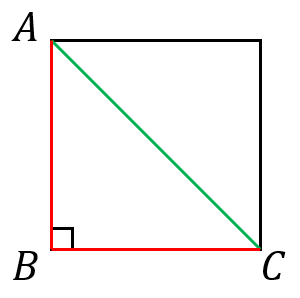



正方形の対角線の長さを求める方法 具体例で学ぶ数学




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun
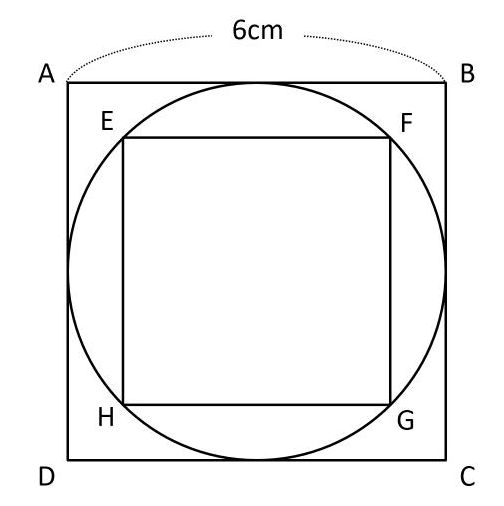



正方形の対角線の長さを求めたい 小学生が算数の知識を使ってどこまでできる 中学受験ナビ
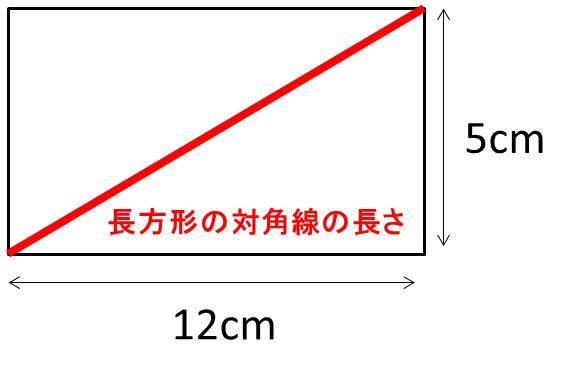



Excel エクセルで対角線の長さを計算する方法 長方形




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
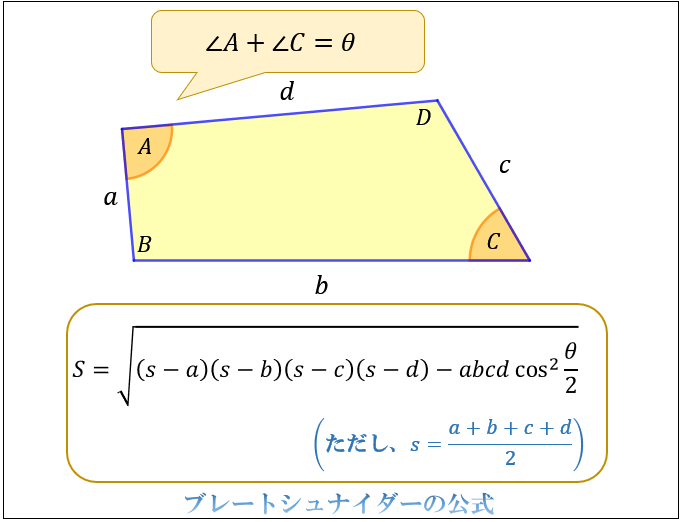



四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
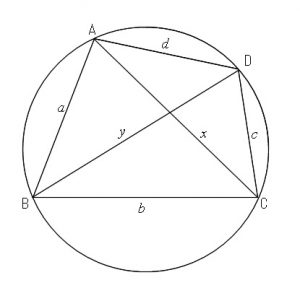



余弦定理を使ったトレミーの定理の証明




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
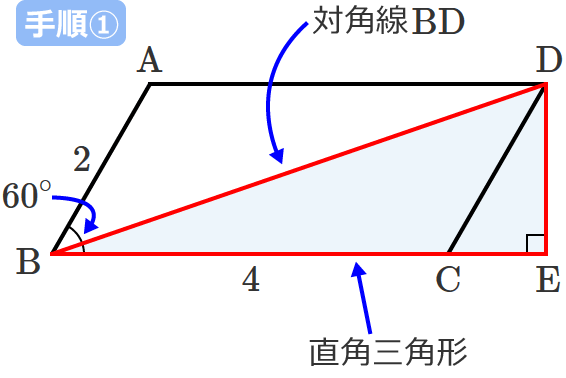



平行四辺形の対角線の長さの求め方
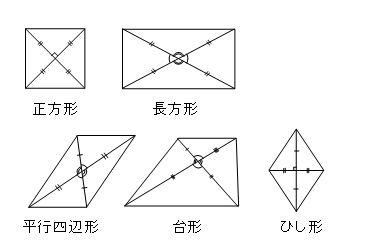



四角形の対角線 レッツスタディー




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




変な質問ですけど この対角線ってそれぞれの角を2等分しているのですか Clear




勉強しよう数学 円に内接する四角形の対角線の交差点までの長さ
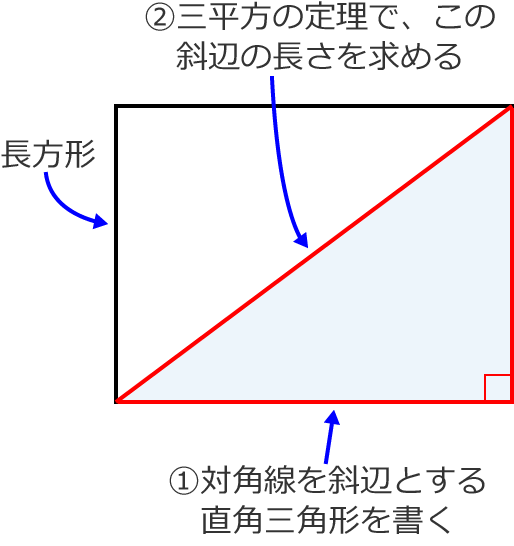



長方形の対角線の長さの求め方



正方形の面積は 1分でわかる公式 対角線 ルートの関係 面積から辺の長さを求める方法
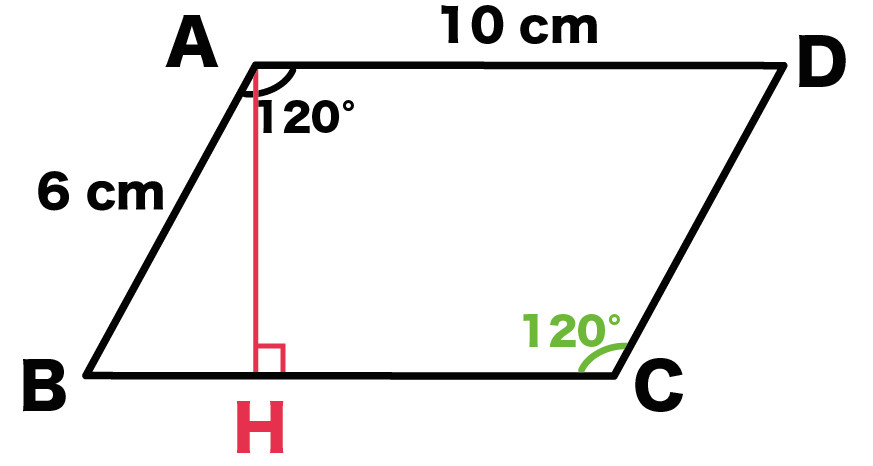



平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
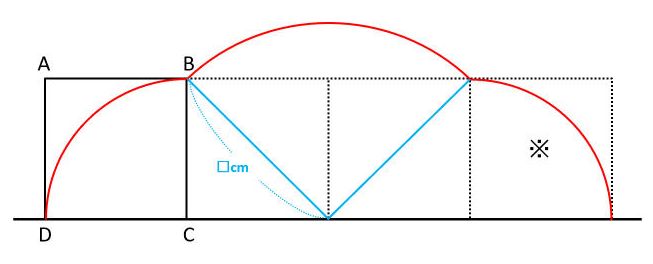



正方形の対角線の長さを求めたい 小学生が算数の知識を使ってどこまでできる 中学受験ナビ



0 件のコメント:
コメントを投稿